什么是光源的光通量？光源的光通量怎么测量？

什么是光源的光通量？在单位时间内，光源向周围空间辐射的使人眼产生光的感觉的能量称为光通量，符号为Ф，单位为流明（lm），简称流。光通量表示光源表面的客观辐射通量对人眼引起的视觉强度。那么，光源的光通量怎么测量？本文对光源光通量的测量原理做了介绍。

什么是光源的光通量？

1.光源光通量的定义

光通量Ф：度量光源在单位时间内向某立体角内辐射的相对视见率的光能量，即人眼所能感觉到的光的辐射功率（辐射能量流速率）的物理量。

Φ=I·Ω

即单位时间某立体角内的光辐射能量与相对视见率的乘积，亦即单位时间某立体角内各波段的辐射能量与该波段相对视见率的乘积之和。

2.光源光通量的单位

（1）光通量的单位为流明lm（lumen）：发光强度为1cd且各方向发光强度均相同的点光源，在1球面度的单位立体角内所发射出的光通量为1流明=1坎德拉·球面度，即1lm = 1cd·sr。

1cd点光源的总光通量为4π流明（因空间立体角共有4π球面度）。

若光源为均匀发光体，则该光源总光通量中Φ总为：

Φ=Ι·Ω=4π·Ι

（2）由于人眼对不同波长之光的相对视见率不同，故此不同波长之光的辐射功率相等时，其光通量并不相等。

例如，波长555nm与650nm之光的辐射功率相等时，前者为后者光通量的10倍。

（3）不计相对视见率的辐射通量的单位为瓦（W）。

若某光源仅辐射555nm波长的光能，且辐射能量为1瓦，则该光源所发出的光通量为683流明。（因1cd为1/683W/st，所以1W相当于683cd·sr即683lm）。

显然实际光源辐射的光谱绝非单一波长，而非555nm波长之光的视见函数又小于1，所以实际光源的光通量一般远比683lm为小。

光源光通量的测量原理：

光源光通量的测量方法有两种：球形光度计法和分布式光度计法。球形光度计法为相对测量方法，测量设备结构简单，测量速度快，在国内检测行业得到了大量应用，但受标准灯尺寸和光强的限制，测量不确定度大，越来越难以满足各级计量检定机构对光源总光通量的测量示值稳定性和精度要求；分布式光度计法为绝对测量方法，绝对测量方法较之相对测量方法拥有更高的计量学价值，更适合作为光源总光通量的基准测量方法。

1.球形光度计法测量原理

球形光度计法，测量器具为积分球。积分球是一个内表面涂有硫酸钡等漫反射材料的球体，原理示意图如下图所示。

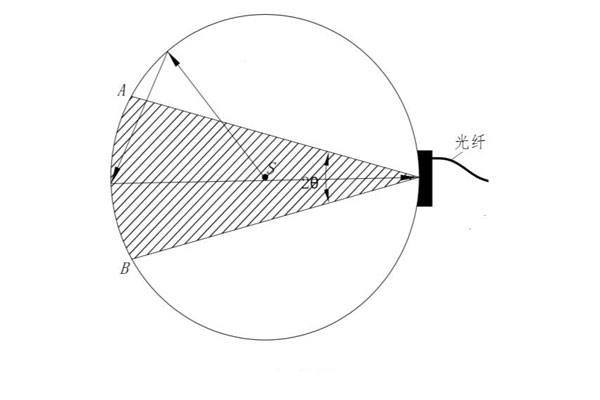
假设S为一固定光源，此固定光源的总光通量大小为Φ，球内壁材料的反射率为ρ，此固定光源照射到球内壁任意微小面元△S的照度值为Ei，i=1，2，3，……n（n→∞），则球面任意面元△S反射的照度值为ρEi，积分球内壁为理想的余弦发光面（发光强度的变化依据余弦规律，即其亮度具有方向无关性），任意面元△S的照度值ρEi，均匀分布于积分球内壁，积分球内壁面积为4πr2，则此微小面元△S作为一个光源经过第一次漫反射所得到的照度值为：

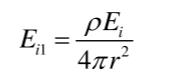
球面任意一个面元△S经过一次漫反射均会发出一次照度Ei1，整个光源经过第一次漫反射后的照度总和为：

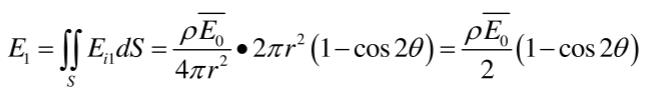
式中：2θ为探测器的光纤管孔径角；S为光纤管孔径角对应曲面域的面积；E0为固定光源照射在积分球内壁任一位置所得到的平均照度值，其大小为：

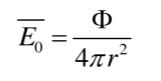
任意面元△S的照度为ρEi，△S作为一个光源经过第二次漫反射产生的照度大小为：

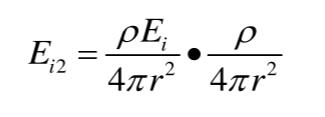
所有微小面元△S经过第2次积分球内壁漫反射后所产生的照度值之和为：

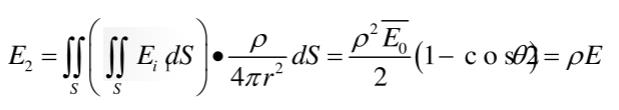
同理，可得整个内壁第3次到第n次每次积分球内壁漫反射后产生的照度总和分别为：

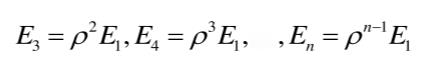
因此，整个积分球内壁经过n次漫反射后所产生的照度值总和为：

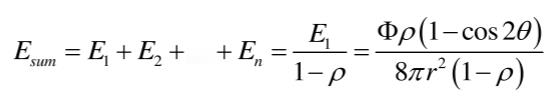
由上式可知标准固定光源和被测固定光源照度值分别为：

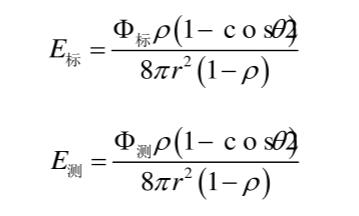
将上面标准固定光源的照度值除以被测固定光源照度值，可得被测固定光源的总光通量为：

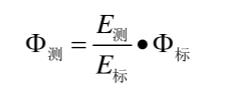
球形光度计法为相对测量方法，必须采用光通量标准灯进行系统定标。光通量标准灯的尺寸、光谱分布，以及量值的大小往往与被测 固定光源存在较大差异，测量结果准确度难以保证。

2.分布式光度计法测量原理

光源总光通量的常用计算方法有三种：球带法、卢素图法、等立体角法。一般采用球带算法计算光源的总光通量。

由式I=dΦ/dΩ可得光强与光通量之间存在如下关系：

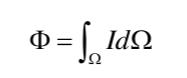
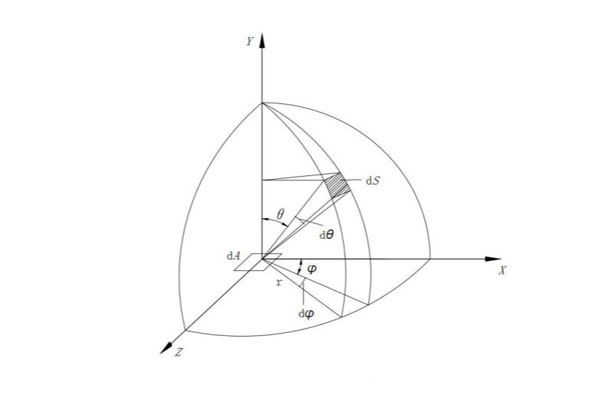
如上图所示，立体角可表示为：

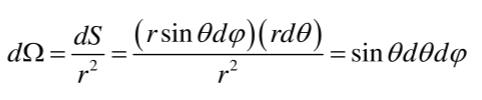
将立体角公式代入光强与光通量之间的关系式后，就可得计算总光通量的公式如下：

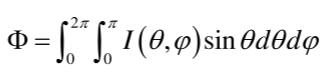
对于轴对称光源：

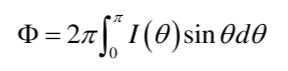
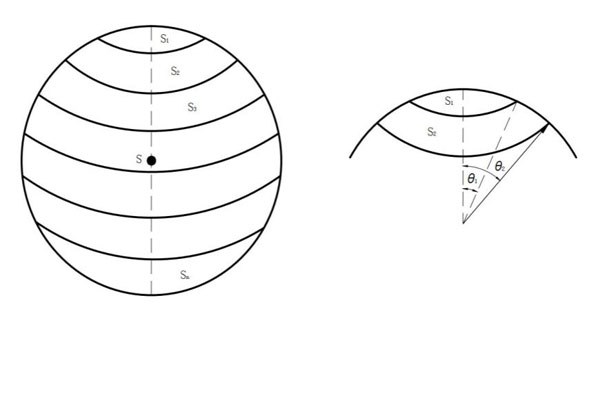
如上图所示，将球面划分为n个大小相等的球带，各球带的发光强度值可分别表示为I1，I2，……In，由上面总光通量计算式可推导得各球带的光通量如下：

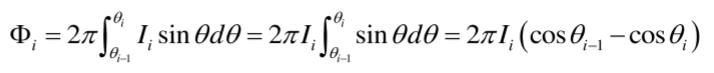
总光通量为：

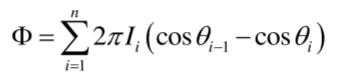
由理论推导过程可知，上式成立的条件是各球带光强为常数：

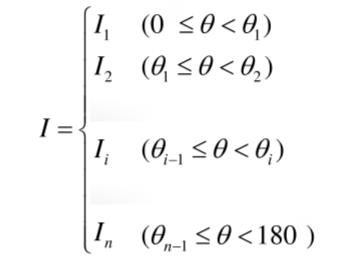
实际上，I随θ成线性变化，设其斜率为k，则任意角的光强大小为：

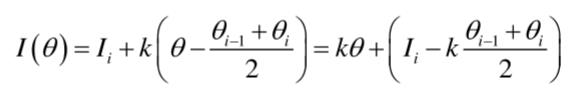
由测量原理可知，分布式光度计法是一种绝对测量方法，不受灯具尺寸等限制，测量精度高，适合作为基准测量方法。